Motion in a Vertical Circle

If velocity given to the block inside tube at bottom level  is $\sqrt{4gl}$ then  velocity at the horizontal level is? ($l=$radius of tube).

A mass of $2.9 kg$ is suspended from a string of length $50 cm$ and is at rest. Another body of mass $100 g$, which is moving horizontally with a velocity of $150 m/s$  strikes and sticks to it. Subsequently, when the string makes an angle of ${60}^{°}$ with the vertical, the tension in the string is:
 ($g=10 m/s^2$).

Find the minimum velocity of the object at the bottom of the point for which the object attached to the string oscillates in the vertical circle.

Minimum velocity given to block so it may complete the circle inside tube.

A ball of mass $1 kg$ moves inside a smooth fixed spherical shell of radius $1 m$ with an initial velocity $v=5 \raisebox{1ex}{$m$}\!\left/ \!\raisebox{-1ex}{$s$}\right.$ from the bottom. What is the total force acting on the particle at point B:

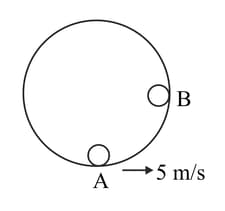
A small box of mass $m$ is kept on a fixed, smooth sphere of radius $R$ at a position where the radius through the box makes an angle of ${30}^0$ with the vertical. The box is released from this position. What is the force exerted by the sphere on the box just after the release?

A particle is suspended from a fixed point by a string of length $5 m$. It is projected from the equilibrium position with such a velocity that the srting slackens after the particle has reached a height $8 m$ above the lowest point. Find the velocity of the particle, just before the string slackens. Find also, to what height the particle can rise further.

A particle moves from rest at $A$ on the surface of a smooth circular cylinder of radius $r$ as shown. At $B$, it leaves the cylinder. The equation relating $\alpha$ and $\beta$ is

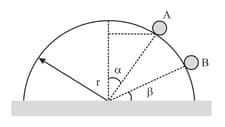
A small block of mass $m$ is pushed on a smooth track from position $A$ with a velocity $\frac{2}{\sqrt{5}}$ times the minimum velocity required to reach point $D$. The block will leave the contact with track at the point where normal force between them becomes zero. Find where the maximum contact force that occurs between the block and the track.

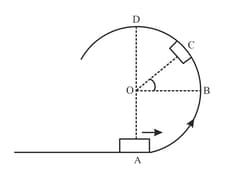
Derive expressions for linear velocity at lowest position for a particle revolving in a vertical circle if it has to just complete circular motion without slackening string.

A point mass $\mathrm{M}$ is hanging by a string of length $\mathrm{l}.$ The velocity $v$ which must be imparted to it in order for it to just barely reach the top is

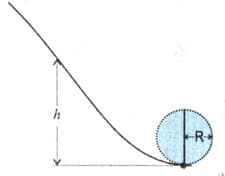
A ball is released from height along the slope and move along a circular track of radius $R$ without falling vertically downwards. Show that $h=\frac{5}{2}R$.

An object of mass $0.5 \mathrm{kg}$ attached to a string of length $0.5 \mathrm{m}$ is whirled in a vertical circle at constant angular speed. If the maximum tension in the string is $5 \mathrm{kg}$ wt, calculate maximum number of revolutions it can complete in a minute.

An object of mass $0.5 \mathrm{kg}$ attached to a string of length $0.5 \mathrm{m}$ is whirled in a vertical circle at constant angular speed. If the maximum tension in the string is $5 \mathrm{kg} \mathrm{wt}$, calculate speed of object.

A stone weighing $1 \mathrm{kg}$ is whirled in a vertical circle attached at the end of a rope of length $0.5 \mathrm{m}$. Find the tension at highest position. 
 

A stone weighing $1 \mathrm{kg}$ is whirled in a vertical circle attached at the end of a rope of length $0.5 \mathrm{m}$. Find the tension at mid position. 
 

A stone weighing $1 \mathrm{kg}$ is whirled in a vertical circle attached at the end of a rope of length $0.5 \mathrm{m}$. Find the tension at lowest position. 
 

Obtain expressions for tension at highest position, midway position and bottom position for an object revolving in a vertical circle.

Derive an expression for difference in tensions at highest and lowest point for a particle performing vertical circular motion.